해당 내용은 Andrew Ng의 Deeplearning ai 강의 C1W2까지에 기반을 두고 있습니다.
Introduction
머신러닝이란 무엇인가?
어떤 알고리즘을 혹은 시스템을 구축할 때 가장 추상적으로 생각할 수 있는 그림은 다음과 같다.
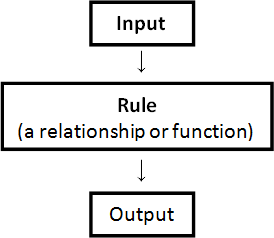
Ref: https://arbs.nzcer.org.nz/algebraic-patterns-and-relationships-different-types-numbers
일반적인 구현에서는 위 그림의 Rule 부분을 개발자들이 직접 코드를 작성한다. 그러나 머신러닝은 Input과 Output 혹은 Input만 가지고 여러 방법론에 의하여 컴퓨터에게 학습을 시킨다. 그렇게 되면, 컴퓨터는 학습을 통해 Rule을 작성하게 된다. 그 후 다음의 Input이 들어왔을 경우 작성한 Rule을 통해 Output을 예측한다.
이는 기존에 사용하던 방법론과는 약간 상반되는 느낌이 있다. 또한, 개발자들이 작성한 Rule은 코드를 볼 수 있기 때문에 틀린 부분을 직접 수정하거나 삭제할 수 있다.
그러나 컴퓨터가 작성한 Rule은 사람이 볼 수 없는 코드이므로 그에 대한 직접적인 수정이 불가하다.
이것이 머신러닝을 흔히 블랙박스라 칭하는 이유다.
House Price Prediction
Data Mining은 주어진 Dataset으로 현재 데이터들의 상관관계를 분석하는 것이다. 여기서 더 나아간 것이 Machine Learning이며, 머신러닝은 분석된 상관관계를 토대로 앞으로 입력될 데이터에 대한 출력을 예측하는 것이다.
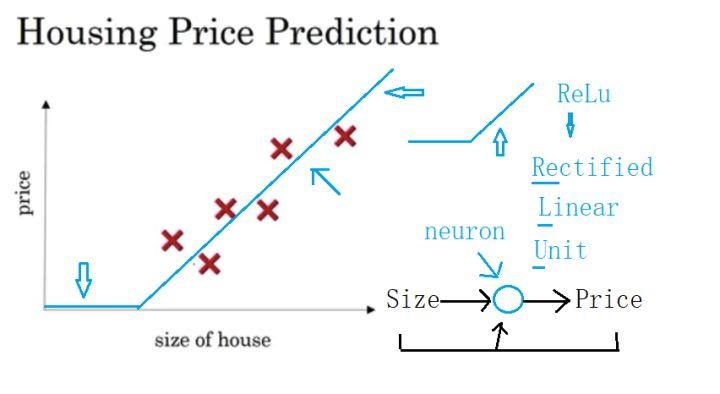
Ref: deeplearning.ai Andrew Ng
집의 크기로 집값을 예측한다고 가정해보자.
집의 크기라는 파라미터에 대한 집값이라는 리턴값은 하나의 점으로 매칭이 가능하다. 수많은 데이터들이 있을 경우 이 점들은 결국 하나의 직선 혹은 곡선으로 수렴할 수 있다.
집의 크기라는 입력과 집값이라는 출력사이에는 하나의 Rule이 있을 것이다.
머신러닝에서는, 특히 Neural Network는 사람의 신경망을 모티브로 만든 방법론이므로 이를 neuron 혹은 perceptron이라 부른다. 그러나 위의 경우, 혹은 대다수의 상황에서, 하나의 변수만으로 집값을 예측한다는 것은 사실 불가능하다. 집의 위치, 방의 개수, 땅값 등등 집값을 예측하는 데에는 많은 변수가 필요하다.
즉, 뉴럴 네트워크는 수많은 뉴런들을 나누어 계산하고 그 결과를 다시 새로운 층에 두어 (한 층을 계산해서 나온 출력들은 다시 하나의 변수가 되므로) 마지막 출력이 나올 때까지 계산하는 방식이 되어야 한다.
이처럼 층이 여러개인 뉴럴 네트워크를 DNN (Deep Neural Network)이라 말하며 이것이 사람들에게 흔히 알려진 Deep Learning이다.
Types of Machine Learning
머신러닝은 구조적으로 크게 3가지 방식이 있다.

Ref: https://www.datasciencecentral.com/profiles/blogs/types-of-machine-learning-algorithms-in-one-picture
Supervised Learning (지도 학습)
지도 학습은 입력과 정답인 출력 레이블 한 쌍을 가지고 학습시키는 방법이다.
지도 학습은 다시 Classification과 Regression으로 분류된다.
Unsupervised Learning (비지도 학습)
비지도 학습은 입력 레이블만을 가지고 학습시키는 방법이다.
지도 학습의 경우에는 정답이 존재하기 때문에 학습 결과와 정답과의 오차를 계산할 수 있으나 비지도 학습은 그렇지 않다. 그렇기 때문에 비지도 학습은 입력 데이터들의 Cluster를 찾아 학습한다.
Reinforcement Learning (강화 학습)
강화 학습은 학습 데이터가 주어지지 않는다. 대신에 학습에 대한 보상(Reward)가 주어지며, 미래에 얻을 보상값들의 평균을 마르코프 의사 결정 과정을 통해 최대로 하는 함수를 찾는 것을 강화 학습이라 한다.
Binary Classification
Classification과 Regression의 가장 큰 차이점은 Classification은 좌표상에서 Discrete하게 표현된다는 것이며, Regression은 Continuous하게 표현된다는 것이다.
즉, Classification은 Cluster를 나누는 기준 선을 찾는 방법이며, Regression은 데이터들이 수렴하게 되는 선을 찾는 것이다.
Classification 중에서 Binary Classification은 정답이 0 혹은 1 두가지로만 구분하는 방법이다. 예를 들어, 64x64의 고양이 사진이 있을 때, 이것이 고양이인지 아닌지만 판별하게 된다.
이를 판별하기 위해서는 64x64인 행렬이 RGB 3채널로 이루어진 사진을 하나의 열벡터로 재배열해야 한다. 이때, 열벡터의 행의 개수는 $64\times64\times3=12288$개가 된다. (이를 $n_x$라 표현) 이 열벡터는 정답레이블에 맞게 변환하는 과정이 필요하다.
선형대수에 따르면 일반적으로 벡터의 변환은 Linear Combination ($v=\alpha_1v_1+\alpha_2v_2+…+\alpha_nv_n$)이며, 벡터에 가중치를 곱한 것들의 합이다. 벡터의 곱은 행렬의 곱으로 표현이 가능하며, 수식은 아래와 같다.
$$z = w^Tx + b$$
그러나 계산되어 나온 $z$는 $0$이나 $1$이 아니다. 그렇기 때문에 Logistic Regression (여기서는 Sigmoid Function)을 사용하여 $0$과 $1$에 근접하게 맵핑하여야 한다. 시그모이드 함수의 범위는 $0<\sigma(z)<1$의 연속된 실수이며, 이것은 확률을 의미한다.
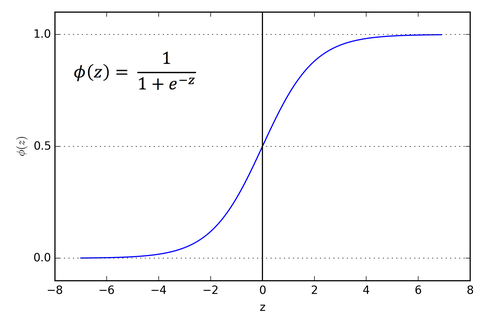
Ref: https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
$\hat{y}=\sigma(z)$이라 하면 $\hat{y}$는 $y$가 $1$인 경우에 대한 확률이며 ($\hat{y}=P(y=1 \mid x)$), 결론적으로 기계는 $\hat{y}$가 $1$에 근접할 수록 고양이라고 판단하는 것이다.
Back Propagation
앞의 과정까지가 Forward Propagation으로 진행되는 방식이다. 그러나 기계가 도출한 답과 실제 정답레이블과의 오차가 클 경우가 많다. 그렇기 때문에 우리는 Forward하게 도출한 답을 토대로 다시 가중치를 수정하면서 오차율을 줄여야 할 필요가 있다.
이를 역전파(Back Propagation)라 한다.
Logistic Regression Cost Function
역전파를 하기 위해 도출된 답과 실제의 답에 대한 오차율을 구해야 한다. 하나에 학습에 대한 오차율 계산 함수를 Loss Function이라 한다. Loss function을 구하는 과정은 다음과 같다.
$$
\begin{aligned}
&if \cr
&&&y = 1: P(y \mid x)=\hat{y} \cr
&else \cr
&&&y = 0: P(y \mid x)=1 - \hat{y}
\end{aligned}
$$
즉, $P(y \mid x)=\hat{y}^y(1 - \hat{y})^{(1 - y)}$가 성립하며, 이에 $\log$를 씌우면,
$$
\log P(y \mid x) = \log\hat{y}^y(1 - \hat{y})^{(1 - y)}
$$
$$
-\mathcal{L}(\hat{y}, y) = y\log\hat{y} + (1 - y)\log(1 - \hat{y})
$$
이 성립한다.
Cost Function은 각 학습 셋에 대한 Loss Function들의 평균이다. 우리는 Cost Function을 구한 후 역전파 과정을 거쳐야 한다.
$$ J(w, b) = -\frac{1}{m}\sum_{i = 1}^m (y_{(i)} \log\hat{y_{(i)}} + (1 - y_{(i)}) \log(1 - \hat{y_{(i)}}))$$
Gradient Descent Algorithm
Gradient Descent는 Cost Function을 최소화하기 위한 가중치를 찾는 알고리즘이다. 이 공식에는 편미분을 이용한다.
미분은 입력에 약간의 변화가 있을 때, 출력이 얼마만큼 변화하는지 확인하기 위함이다.
즉, $f(x)=2x$에 대해서 $x_1=1$일 때, $f(x_1)=2$이며, $x_2=1.001$일 때, $f(x_2)=2.002$이다.
이 경우 $f(x)$의 도함수 $f^\prime(x)$는 $\frac{0.002}{0.001}$이므로 $2$가된다.
편미분은 미분의 일종으로 입력 파라미터가 하나가 아닌 여러개일 때, 한 파라미터가 약간 변했을 때 출력이 얼마만큼 변화하는 지를 나타내는 것이다.
위에서는 $J(w,b)$를 $w$에서 편미분하는 것을 $\frac{\partial J(w,b)}{\partial w}$로 표현하며, 마찬가지로 $b$에 대해 편미분하면 $\frac{\partial J(w,b)}{\partial b}$로 표현한다.
Gradient Descent는 볼록한(convex) 함수가 있을 때 이 함수의 가장 아래 부분으로 점차 결과물을 내리는 방식이다. 오차율 함수 $J(w,b)$는 하단으로 갈수록 오차율이 적어지는 것을 의미한다.
$$
\begin{aligned}
w:=w-\alpha\frac{\partial J(w,b)}{\partial w} \
b:=b-\alpha\frac{\partial J(w,b)}{\partial b} \
\end{aligned}
$$
위 Gradient Decsent를 각 $w,b$에 적용하여 가장 낮은 오차율이 나오도록 $w$와 $b$를 수정하는 작업이다. ($\alpha$는 learning rate을 의미)
추가적으로 Linear Regression에서의 Cost Function은 Euclidean Distance를 응용한 Mean Squared Error
$$J(w,b)=\frac{1}{m}\sum_{i=1}^m\frac{1}{2}(\hat{y}-y)^2$$
를 사용하지만, Logisitc Regression에서 MSE를 사용하면 Convex하지 않은 함수가 나온다. 그렇기 때문에 위와 같은 방법을 사용하는데 이를 Cross Entropy Error라고 한다.
Back Propagation 수행 시에는 Gradient Descent를 위한 편미분을 계산하게 되는데 위의 Binary Classification 예제는 단층 레이어 구조의 뉴럴 네트워크를 사용하기 때문에 편미분 유도가 용이하다.
그러나 Deep Learning은 Multi Layer 구조이므로 편미분을 구할 때 다소 복잡하다. 그렇기 때문에 각 층의 출력에 대해 한 단계씩 뒤로 가면서 각각의 편미분을 구하는 일을 반복하게 된다. 이를 Chain Rule이라 한다.
