자료구조, 힙(Heap)

Complete Binary Tree

Tree에 대한 기본적인 설명은 루비콘 팀 Martin Kim의 포스트를 참조한다. 🙇

Ref: https://blog.martinwork.co.kr/theory/2018/09/22/what-is-tree.html

추가적으로 Tree에 대해 부가설명을 덧붙인다.
Tree의 정의는 다음 2가지를 따른다.

1. A root node
2. The remaining nodes are partitioned into $n(n \geq 0)$ disjoint sets $T_1, T_2, … , T_n$ ($T_i$ : subtrees of the root)

즉, 루트 노드가 존재하며, 0개 이상의 서브트리로 분리된 노드가 존재해야 한다.
이 중 Full Binary Tree는 Depth가 $k$일 때, 총 노드의 개수는 $2^k - 1$개인 트리이며,
Complete Binary Tree는 Depth가 $k$인 Full Binary Tree를 왼쪽에서부터 순차적으로 읽었을 때, $k-level$에서 Complete Binary Tree의 총 노드 수 $n$의 인덱스를 가진 노드가 존재하는 것을 말한다.

이 때, $k =\lceil\log_{2}(n + 1)\rceil$이 성립한다.
Complete Binary Tree는 마지막 레벨을 제외하고 모든 레벨이 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있기 때문에 공간의 낭비가 없어 배열로 구현하는 것이 효율적이다.

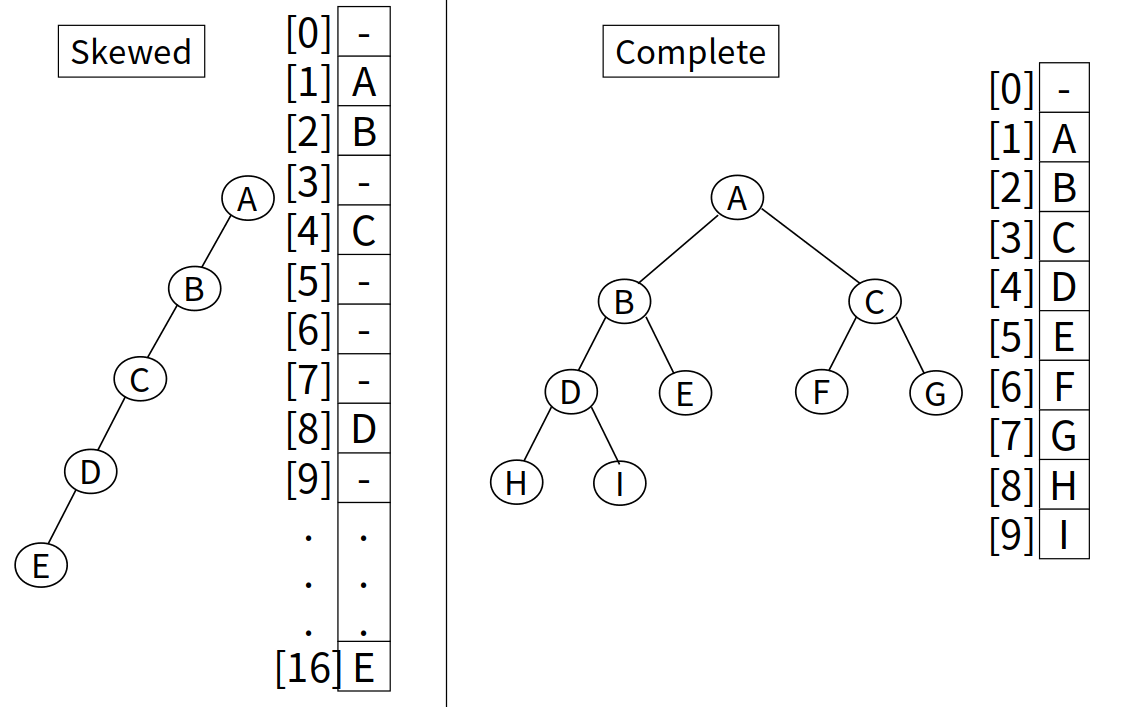
배열로 구현 시, $i$번째 노드의 자식 노드는 각각 $2i,\ 2i + 1$이 되며, 부모 노드는 존재 시 $\lfloor i / 2\rfloor$가 된다. (부모 노드의 인덱스가 $0$부터 시작할 경우에는 자식은 $2i + 1,\ 2i + 2$, 부모는 $\lfloor(i - 1) / 2\rfloor$가 된다.)

Heap의 정의와 연산

사전적 의미에서 Heap은 무엇인가를 차곡차곡 쌓아올린 더미를 뜻한다.
Heap은 메모리에서 동적할당을 받을 때, 정렬을 할 때, 그리고 우선순위 큐(Priority Queue)나 무손실 압축 알고리즘인 허프만 코드 등에 다양하게 사용된다.

위에서 Tree를 설명한 이유는 Heap은 Tree 구조 중 Complete Binary Tree에서 몇가지 Constraint를 더하여 파생된 자료구조기 때문이다.
Heap은 Max Heap과 Min Heap 두가지가 있는데, Max Heap은 Complete Binary Tree이면서 노드의 값이 자식 노드의 값보다 작지 않은 경우, Min Heap은 그 반대의 경우다.

Heap이 Complete Binary Tree를 이용하여 구현된 이유는 삽입과 삭제의 속도 때문인데, 앞서 설명 한 Complete Binary Tree에서 부모와 자식 노드의 인덱스를 빠르게 찾을 수 있는 특성 때문이다.

이 글에서는 Max Heap을 기준으로 설명한다.
Heap을 C++의 Class를 사용하여 정의하면 다음과 같다.

class MaxHeap{
public:
    MaxHeap();
    ~MaxHeap();
    void Insert(int x); //Push the element
    void Delete(); //Pop the root
    int Top(); //Return the root
    int Top(int n); //return the n-th rank node
    bool isEmpty(); //Determine the heap is empty or not
private:
    vector<int> heap; //Index 0 is not used
};

Heap의 삽입 연산의 경우 Complete Binary Tree의 특성에 따라 처음에는 Leaf 노드의 빈 곳 중 가장 왼쪽에 새로운 노드를 추가한다.
그 후, 삽입된 노드와 그 노드의 부모와 비교 연산을 수행하고 삽입된 노드의 값이 가장 크면 부모 노드와 자리를 바꾼다.

그리고 옮겨진 상태에서 다시 부모와 비교, Swap을 수행하며, 부모보다 값이 크지 않다면 삽입연산이 종료된다.
그렇지 않을 경우 계속된 과정 끝에 삽입된 노드가 루트가 되며 삽입연산이 종료된다.
이 과정을 Bubble up(거품이 올라가는 모양과 유사하여)이라 칭한다.

삽입 연산을 도식화 한 경우는 다음과 같다.

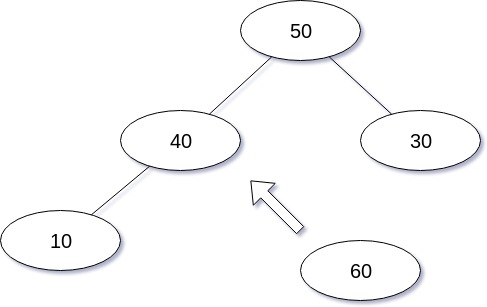
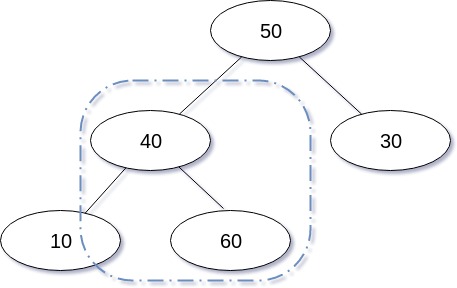
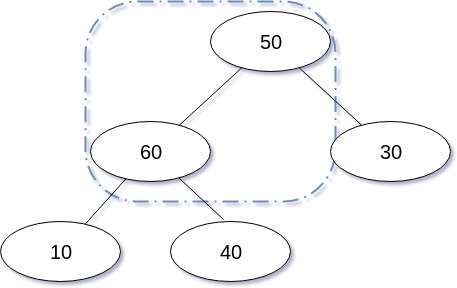
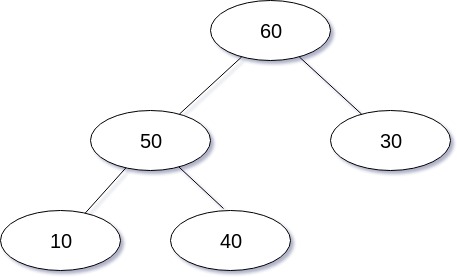
삽입 연산을 구현한 코드는 다음과 같다.

void MaxHeap::Insert(int x) {
    if(isEmpty())
        heap.push_back(x);
    else{
        heap.push_back(x);
        int i = heap.size() - 1;
        while(i != 1){
            if(heap.at(i) > heap.at(i / 2))
                swap(heap.at(i), heap.at(i / 2));
            else
                break;
            i /= 2;
        } //bubble up
    }
}

삭제 연산의 경우는 별도의 인덱스를 지정하는 것이 아니라, 루트 노드에 대한 연산이다.
루트 노드를 Pop한 후에, 가장 마지막 노드를 루트로 올린다.

그리고 자신과 두 자식(혹은 한 자식)과 비교연산을 수행한 후 가장 큰 노드를 해당 노드와 Swap한다.
그 후, 삽입 연산과 마찬가지로 모두 적절한 자리에 놓일 때까지 반복작업을 수행한다.

이 과정을 Trickle Down(물방울이 떨어지는 모양과 유사하여)이라 칭한다.
삭제 연산을 도식화 한 경우는 다음과 같다.

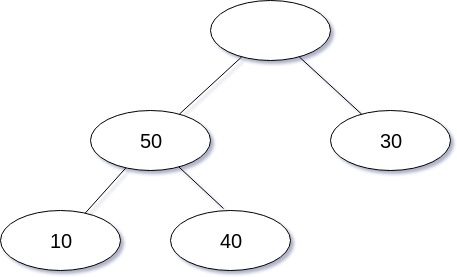
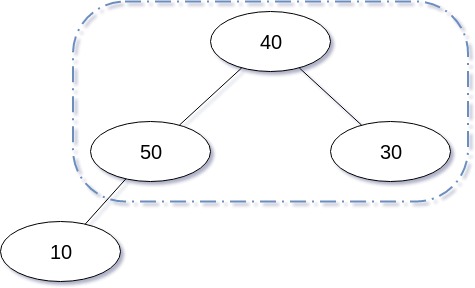
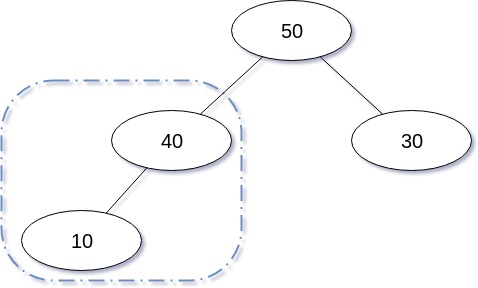
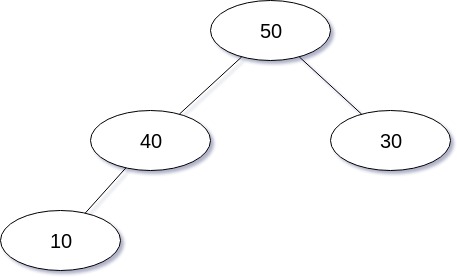
삭제 연산을 구현한 코드는 다음과 같다.

void MaxHeap::Delete() {
    if(isEmpty())
        throw "error";

    heap.at(1) = heap.at(heap.size() - 1);
    heap.pop_back();
    int i = 1;
    int last_idx = heap.size() - 1;
    int max_child_idx;
    while(i * 2 <= last_idx){
        if(i * 2 + 1 > last_idx) //if child of i is only left side
            max_child_idx = i * 2;
        else{
            if(heap.at(i * 2) > heap.at(i * 2 + 1)) //compare left-child to right-child  before child to parent
                max_child_idx = i * 2;
            else
                max_child_idx = i * 2 + 1;
        }

        if(heap.at(i) < heap.at(max_child_idx)) //compare child to parent
            swap(heap.at(i), heap.at(max_child_idx));
        else
            break;
        i = max_child_idx;
    } //trickle down
}

삽입과 삭제는 트리의 높이만큼의 시간의 소요되므로 이는 $O(\log_{2}n) $이다.
Heap에 가장 중요한 연산은 삽입과 삭제 두가지이나, 추가적으로 n번째로 큰 수를 리턴해주는 Ranking Search가 가능하며, 이 경우 Heap을 이용한 정렬인 Heap Sort가 사용된다.

Heap Sort는 힙이 비게 될 때까지, Top 연산(트리의 루트노드를 리턴)과 삭제 연산을 계속해서 수행하면서 Top 연산에서 리턴받은 값들을 차례로 새로운 배열에 저장하면 정렬이 되는 방식이다.
Heap Sort를 수행한 후 완성된 배열의 n번째 인덱스가 곧 힙에서 n번째로 큰 수를 의미한다.

Ranking Search에 대한 코드는 다음과 같다.

//using heapsort
int MaxHeap::Top(int n) {
    if(heap.size() - 1 < n)
        throw "error";

    vector<int> backup = heap;
    vector<int> sorted_heap;
    sorted_heap.push_back(0);
    int top;
    while(!isEmpty()){
        top = Top();
        Delete();
        sorted_heap.push_back(top);
    }
    heap.swap(backup);

    return sorted_heap.at(n);
}

사실 위에 while문을 n번만큼만 돌아도 Ranking Search가 가능하지만, Heap Sort의 설명을 곁들이기 위해서 모든 노드를 비웠다. Heap Sort의 경우에는 $O(n\log_{2}n)$의 수행시간을 보인다.